本文阐述了 AQuiz 推荐算法的原理及基本实现。

1. 摘要

   AQuiz 是为 ArRow 设计的推荐算法，前身为原 XFCRC。

   通过 AQuiz，可以快速地得到项得分、分区内项排列、分区排列与全局项排列，且具有生态性。

2. 目录

   • 综述

   • 原理

     • 分区内项排列

     • 分区排列

     • 全局项排列

       • 分区权重

       • 群权重

       • 环比惯性

       • 结论

     • 总结

   • 实现

3. 综述

   AQuiz 是为 ArRow 设计的推荐算法，前身为原 XFCRC。

   AQuiz 的强制条件：项有明确分区（可多个）；有浏览量且确定来源用户；有认可量（如点赞，可多种）。

   在 AQuiz 算法中，优秀项不等同于优先项，最终得到的相对分数排列以优先项为序，绝对分数则能反映项的优秀程度。

4. 原理

   1. 分区内项排列

      设浏览量 v、认可量 r。

      一般地，单分区内，浏览量、认可量（若有多种则对每一种认可量按下述过程求 s 后得总积）与认可率 q 分别降序排列后，均近似于正态分布。浏览量即样本量，认可率反应项的质量。

      对于任意分区，认可率 q 符合：

      $$\begin{array}{}\text{(2)}& n～N({\mu }_q,{\sigma }_q)\end{array}$$

      认可率期望值为：

      $$\begin{array}{}\text{(3)}& {\mu }_q=\frac{\sum _{i=1}^n{r}_i}{\sum _{j=1}^n{v}_j}\end{array}$$

      其中 n 为项的总数。

      或近似于：

      $$\begin{array}{}\text{(4)}& {\mu }_q=\frac{q_{max}-q_{min}}{2}\end{array}$$

      浏览量过小时，认可率置信度 1-α 下降，反解以下方程使样本量小于阈值 t 的可能性为 p (p<0.5)：

      $$\begin{array}{}\text{(5)}& f(t_v)=\frac{1}{\sqrt{2\pi }{\sigma }_v}\exp (-\frac{(t_v-{\mu }_v{)}^2}{2{{\sigma }_v}^2})=0.5-p\end{array}$$

      得

      $$\begin{array}{}\text{(6)}& t_v=\sqrt{-2{{\sigma }_v}^2\cdot {\log }_e((0.5-p)\cdot \sqrt{2\pi }{\sigma }_v)}-{\mu }_v\end{array}$$

      α 为函数：

      $$\begin{array}{}\text{(7)}& \begin{array}{c}\alpha (v)=\{\begin{array}{l}\frac{v}{t_v}(0⩽v⩽t_v)\\ 1(v⩾t_v)\end{array}\end{array}\end{array}$$

      阈值左侧区间内置信度从 0 向右递增于阈值处为 1，置信度为 0 时认可率默认为期望值，得式 (1)。

      $$\begin{array}{}\text{(8)}& \begin{array}{c}{q^{\prime }}_i=\alpha (v_i)q_i+{\mu }_q(1-\alpha (v_i))\\ {q^{\prime }}_i=\alpha (v_i)(q_i-{\mu }_q)+{\mu }_q\\ (1)\end{array}\end{array}$$

      对于任意单项，其得分 s 为与认可率期望值的比值的百分比，如式 (2)。

      $$\begin{array}{}\text{(9)}& \begin{array}{c}{s}_i=\frac{{q^{\prime }}_i}{{\mu }_q}\cdot 100\mathrm{\%}\\ (2)\end{array}\end{array}$$

      得分 s 与分区内项优先度成正比，同时也是项在全局中的绝对得分，因此将 s 降序排列得集合 A，将项按 s 降序排列得集合 A'，A' 即分区内项有序列，索引越小优先度越高。

   2. 分区排列

      一个分区的平均浏览量反应分区热度，理想状态下，各分区热度相同，因此为平衡分区热度，分区优先度与分区热度成反比，因此将平均浏览量升序排列得集合 B，将分区按平均浏览量降序排列得集合 B‘，B' 即分区有序列，索引越小优先度越高。

   3. 全局项排列

      对于全局项排列，需要考虑的因素较多，本文细述分区权重、群权重、环比惯性。

      1. 分区权重

         分区权重规定了用户在某一分区中投入的注意力的目标量，目标量越高，加权越大。

         设每一用户总注意力为 1，则任意分区权重 w 符合：

         $$\begin{array}{}\text{(10)}& \frac{1}{2n}<w<\frac{1}{n}\end{array}$$

         其中 n 为分区总数。

         上式等价于：

         $$\begin{array}{}\text{(11)}& \frac{w_1}{2}<w_2<2w_1\end{array}$$

         一用户对于分区 i 有总阅读量 v'、（总）认可量 r'。为了使系统流动，最不感兴趣的应与最感兴趣的权重相同。分区 i 得分为：

         $$\begin{array}{}\text{(12)}& s_i={v^{\prime }}_i+{r^{\prime }}_i\end{array}$$

         所有分区的 s 降序排列得集合 S。

         则得分最高的分区 0 、最低的分区 n、中位分区 n/2 分别可在平面直角坐标系中表示为：

         $$\begin{array}{}\text{(13)}& P(S_0,1),Q(S_{n-1},1),M(S_{\frac{n}{2}},0)\end{array}$$

         过点 P、Q、M 作抛物线，得解析式：

         $$\begin{array}{}\text{(14)}& \begin{array}{c}f(x)=a{x}^2+bx+c\\ 1=a{S_{\frac{n}{2}}}^2\\ a={S_{\frac{n}{2}}}^{-2}\\ f(x)={S_{\frac{n}{2}}}^{-2}(x^2-(S_0+S_n)x+S_0{S}_n+{S_{\frac{n}{2}}}^2)\end{array}\end{array}$$

         即

         $$\begin{array}{}\text{(15)}& w_i={S_{\frac{n}{2}}}^{-2}({s_i}^2-(S_0+S_n)s_i+S_0{S}_n+{S_{\frac{n}{2}}}^2)\end{array}$$

         加入分区优先度加权得 w'：

         $$\begin{array}{}\text{(16)}& {w^{\prime }}_i=\frac{B_0}{B_i}\cdot {S_{\frac{n}{2}}}^{-2}({s_i}^2-(S_0+S_n)s_i+S_0{S}_n+{S_{\frac{n}{2}}}^2)\end{array}$$

      2. 群权重

         群权重是分区权重在全局用户中的衍生，它通过其他用户与目标用户的相似性，描述了目标用户可能对项感兴趣的可能性（标准值100%）。

         对于每一用户，存在一个势为 n 的有限集：

         $$\begin{array}{}\text{(17)}& C=\{x|x_i={w^{\prime }}_i\}\end{array}$$

         它量化了用户分区偏好，可以转换为 n 维笛卡尔坐标系中一点 U：

         $$\begin{array}{}\text{(18)}& U(C_0,C_1,C_2,...,C_n)\end{array}$$

         等价于：

         $$\begin{array}{}\text{(19)}& U({w^{\prime }}_0,{w^{\prime }}_1,{w^{\prime }}_2,...,{w^{\prime }}_n)\end{array}$$

         将所有 U 点按感兴趣的分区分为 n 类且一一对应，称为用户组，如用户组0即对分区0感兴趣的用户。

         一般而言，用户组间存在交集，如果确定交集为空，可以使用 EM模型聚类 等聚类分析模型进行单一归类，本文仅细述前者。

         对于用户组 j，其中几何中心坐标可表示为集合：

         $$\begin{array}{}\text{(20)}& \begin{array}{c}{O}_j=\{x|x_i=\{\begin{array}{l}0(i\ne j)\\ 1(i=j)\end{array}\}\end{array}\end{array}$$

         对于一个 U 点，其在用户组 j 中的典型性 m 与它到用户组 j 中心的直线距离 d 的函数关系如下图：

         

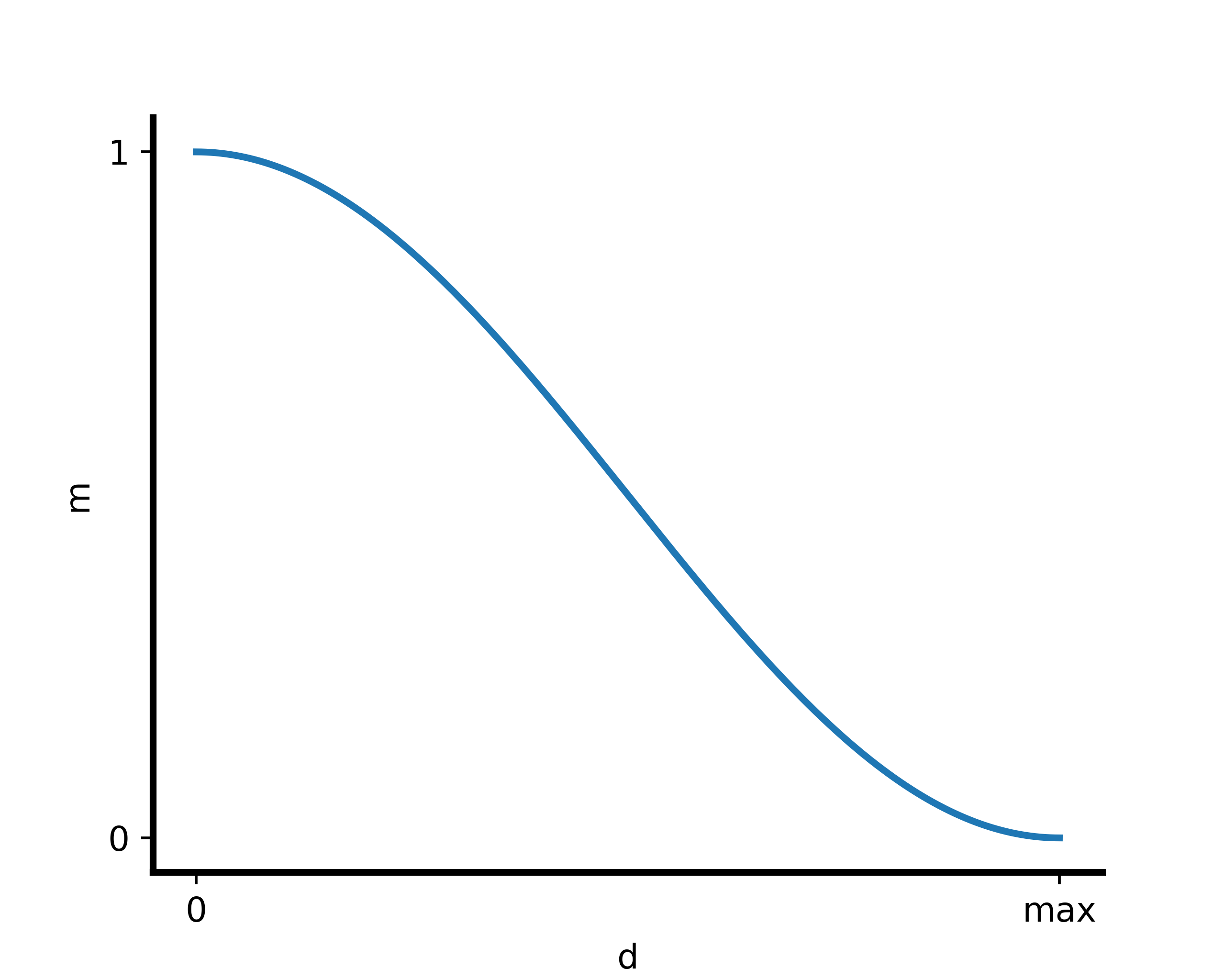
         其解析式为：

         $$\begin{array}{}\text{(21)}& \begin{array}{c}{m}_j=\cos \frac{d_j\pi }{2d_{j-max}}+\frac{1}{2}\\ d_j\in \{0,d_{j-max}\}\end{array}\end{array}$$

         其中 d 有下式：

         $$\begin{array}{}\text{(22)}& d_j=\sqrt{\sum _{i=0}^n(C_i-{O_j}_i{)}^2}\end{array}$$

         d 的最大值为任意 U 点到用户组 j 中心的最大距离。

         现有用户1与2，用户1浏览了一分区 j 的子项，则对于用户2，此项来自用户1的群加权得：

         $$\begin{array}{}\text{(23)}& w_1=\frac{1+{m_j}_1}{{m_j}_2}\end{array}$$

         仅对于用户2，此项的群加权 w' 为来自所有其他浏览了此项的用户的群加权之积：

         $$\begin{array}{}\text{(24)}& w^{\prime }=\prod _i{w}_i\end{array}$$

      3. 环比惯性

         假定一项的热度自发布后存在一定自然趋势，如图：

         

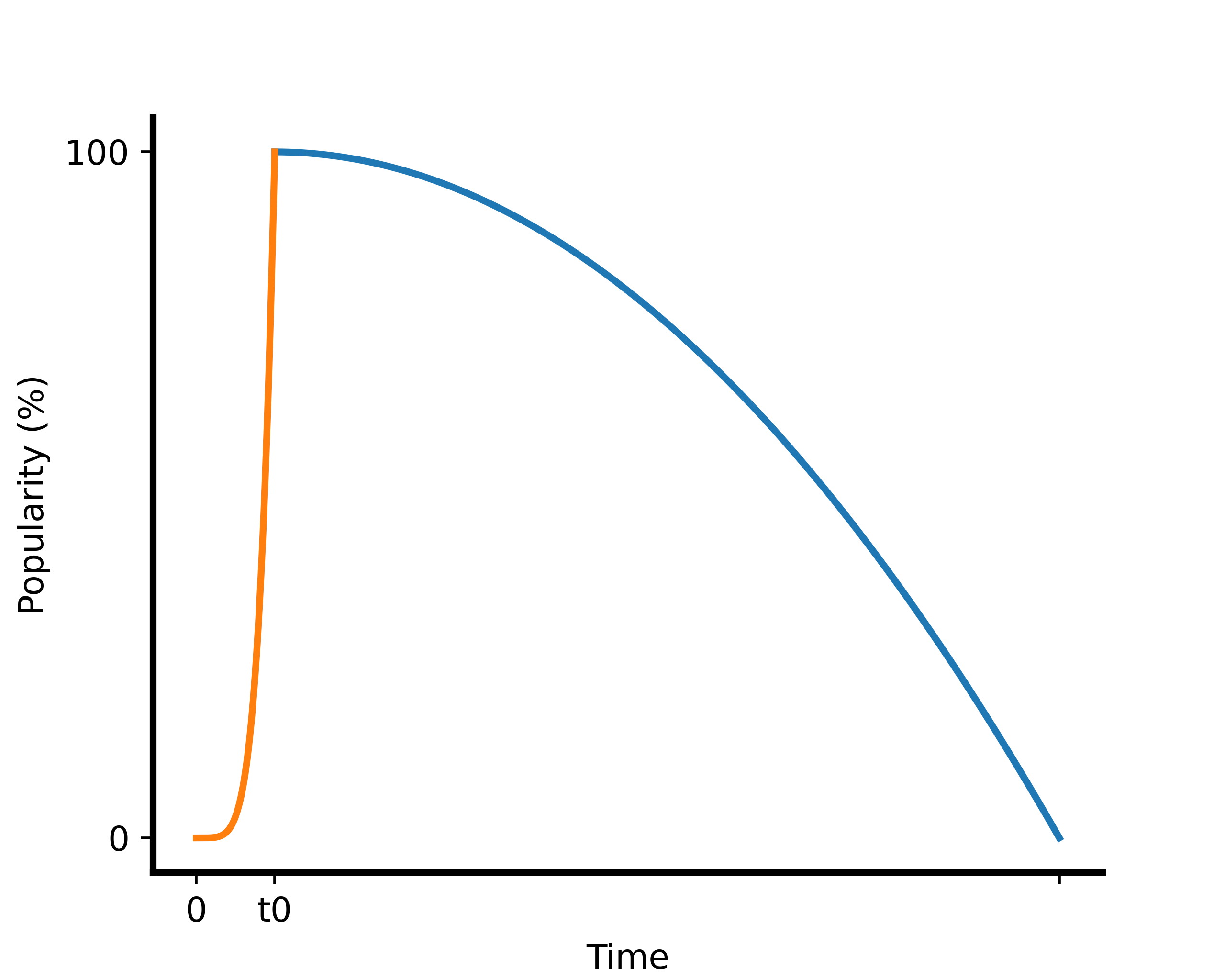
         设解析式：

         $$\begin{array}{}\text{(25)}& p-t:y=f(t)\end{array}$$

         时刻 t 的浏览量环比目标值 G 符合：

         $$\begin{array}{}\text{(26)}& G_t=\frac{v_t-v_{t-1}}{v_{t-1}}\cdot 100=f(t)\end{array}$$

         设实际浏览量环比 g，则加权 w 得：

         $$\begin{array}{}\text{(27)}& w=(100+G_t-g_t)\mathrm{\%}\end{array}$$

      4. 结论

         一项对于一用户，其相对得分 ß 为这一项的分区内得分 s、这一项所属分区的分区权重 w'、此项对于此用户得到的群加权 w'、环比惯性加权 w 的积。对于匿名者，不含后两因数。

         若一项属于多个分区，则其得分为它作为它所属的每一分区的子项的得分之积。

         将项按 ß 降序排列得集合 I'，即全局项有序列，索引越小优先度越高。

   4. 总结

      以上所有算法都基于每一分区的认可率期望值均为正数，若初始条件不符合可以加入混淆项以改动认可率期望值。

      若样本量过少或极度偏离正态分布，会造成部分功能失效。

5. 实现

   略。